Unit 10 Recursion
Intro to Recursion
- 5-7.5% of the AP Exam, mainly in the multiple choice section
- A recursive method is method that calls itself.
- It contains at least one base case that halts recursion and once recursive call
- Each recursive call has own local variables
- Parameter values take progress of recursive process
- A recursion can be replaced with an iterative and give the same result
- Recursion can traverse String, array, and ArrayList objects
This is what a recursion looks like where the example method is called within itself.
public static void example(int n) {
if (n > 0)
example (n-1);
}
In this example, the simplerRecur method is called within itself. So, simplerRecur(4) will result in printing 4 and then one less than it until the parameter is false. It then cycles back up to the top of the call stack. This is why it returns the 2 3 4 at the end.
public static void simplerRecur(int n) {
System.out.println(n);
if (n > 2)
simplerRecur(n-1);
System.out.println(n);
}
simplerRecur(4);
In this, simpleRecur2(8) wil return 8 + simpleRecur2(4) and simpleRecur2(4) will return 4 + simpleRecur2(2). This process will continue until n = 0 and all the values will be added together.
8 + 4 + 2 + 1 + 0
public static int simpleRecur2(int n) {
if (n == 0)
return 0;
return n + simpleRecur2(n/2);
}
simpleRecur2(8);
This one is similar to the last example where it will add the values together but this has multiple recursive methods inside it. So, dblRecur(5) will return 5 + dblRecur(2) + dblRecur(1) and then dblRecur(2) and dblRecur(1) will have their own run through the method until n is no longer greater than 0.
public int dblRecur(int n) {
if (n > 0)
return n + dblRecur(n/2) + dblRecur(n/3);
return 0;
}
dblRecur(5);
Recursion can also be seen will String objects. In this, mystery("computer") will first go through the mystery(s.substring(2)) which will result in a call stack with "computer", "mputer", "uter", "er", and " ". THe print statement will then print the first letter of those Strings so e u m c.
public static void mystery (String s) {
if (s.length() > 1) {
mystery(s.substring(2));
System.out.print(s.substring(0,1));
}
}
mystery("computer");
10.2 Binary Search With Equations
We start by taking the entire array, starting with the first and the last numbers, and find the midpoint. Starting number is 0, and end is 40, and the midpoint is 20.

Since 24 is greater than 20, we take the upper bound of the list, ignoring everything less that 22.The first number now becomes 22.
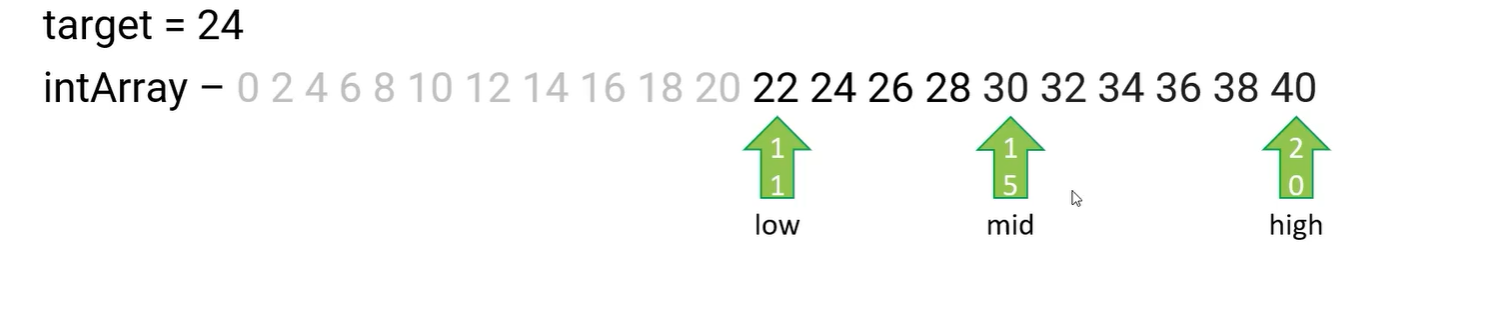
We identify the midpoint again, which is 30. Since the new midpoint is higher than 24, we now take the lower bound. Here, the last number becomes 28.

In this new bound, we find the midpoint again, which happens to be 24. So, we have found our target.
Now, lets say that the target was 23, instead of 24. The program would have to keep going from the midpoint of 24. Since 23 is less than 24, it takes the lower bound. However, this makes first, last and midpoint numbers 22.
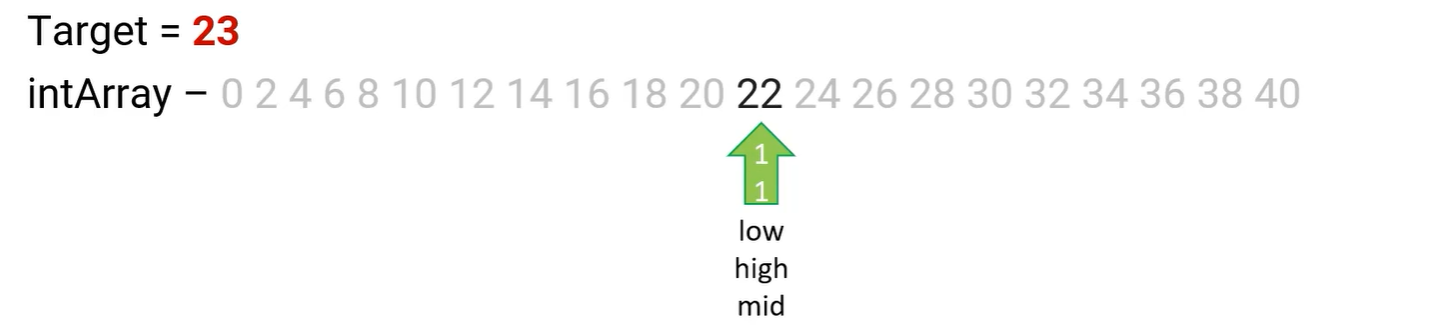
Again, since 22 is less than 23, the first number becomes 24, and the last number stays 22. This becomes a problem since the first number is greater than the last, which is our base case. This tells the program that the number 23 isn’t in the list, and that it should end.

public class recursion{
public static int recursionBinarySearch(int[] array, int first, int last, int target){
int midpoint;
//if the first number is greater than the last, the target number is not in the list
if (first > last){
System.out.println(-1);
return -1;
}
else{
midpoint = (first+last)/2;
//take the upper bound if number is greater than midpoint
if (array[midpoint] < target){
return recursionBinarySearch(array, midpoint+1, last, target);
}
// take the lower bound if the number is lesser than midpoint
if (array[midpoint] > target){
return recursionBinarySearch(array, first,midpoint-1, target);
}
System.out.println("index of target: " + midpoint);
return midpoint;
}
}
public static void main(String[] args){
// test array in main
int[] test_array = new int[]{ 0,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40 };
recursion.recursionBinarySearch(test_array, 0, test_array.length, 24);
}
}
recursion.main(null);
Merge Sort
-
Merge Sort can be used to sort ArrayLists
-
Uses a Divide and Conquer algorithm to Sort ArrayList
- Divides the array into halves, and then calls itself for the two different halves in order to sort them
- merges the two sorted halves into one lists
-
Merging Values into One Sorted Array
- copy the original elements into a temporary array
- work from left to right in each virtual array to compare element and return them to the correct order in the original array
Way to Think About It: mergeSort (myList) { mergeSort(left); mergeSort(right); mergeSort (left & right) }
First, the mergeSort function splits the ArrayList into half, and then takes the left side of the list. It then calls mergeSort again and then halves the list, and does this two more times. Eventually, it is left with just 5 after sorting using all of mergeSort(left).
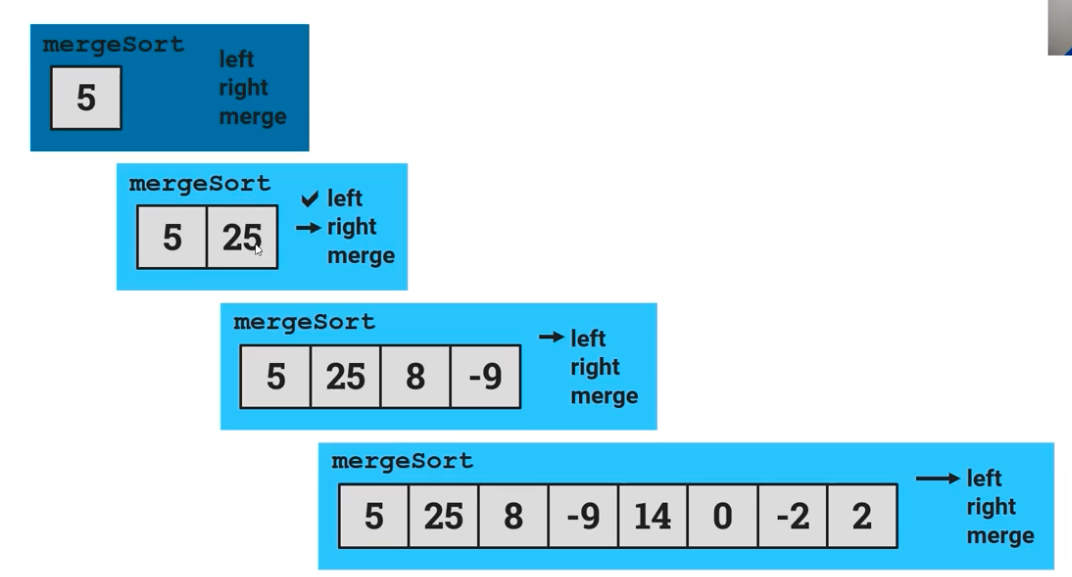
Then, it goes back to the third step with just the 5 and 25, and looks at the right side of that one section. It compares the two halves, 5 and 25, and then sorts it, keeping the 5 before the 25 and recurses its way back to the ArrayList in the beginning.
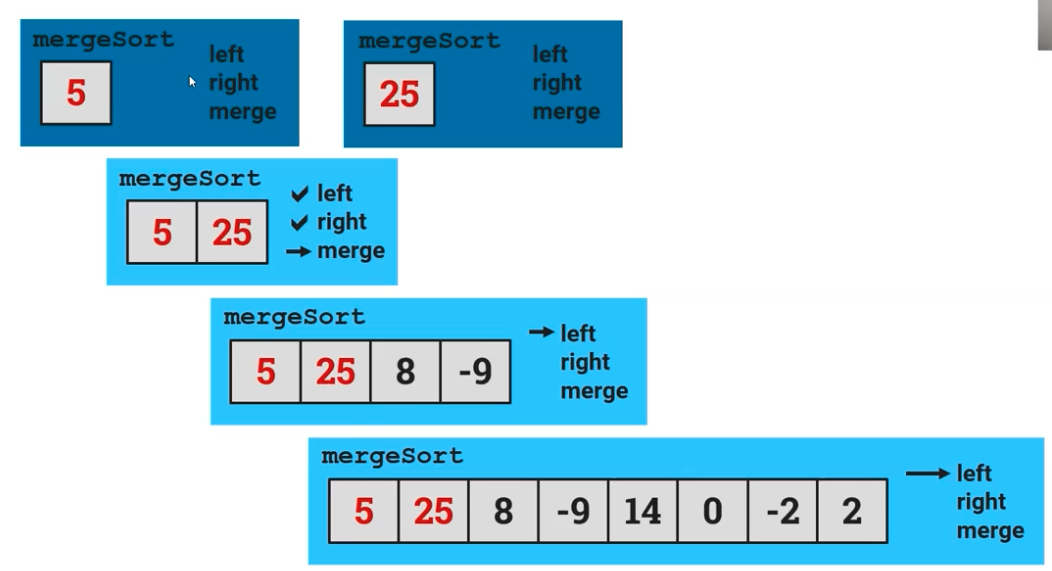
We then go back down one more half where we have the 5, 25, 8, and -9. Because we had already sorted the left side of that list, we then go to the right side with the 8 and -9. We then sort the left side where we get 8 and then the right side with -9.
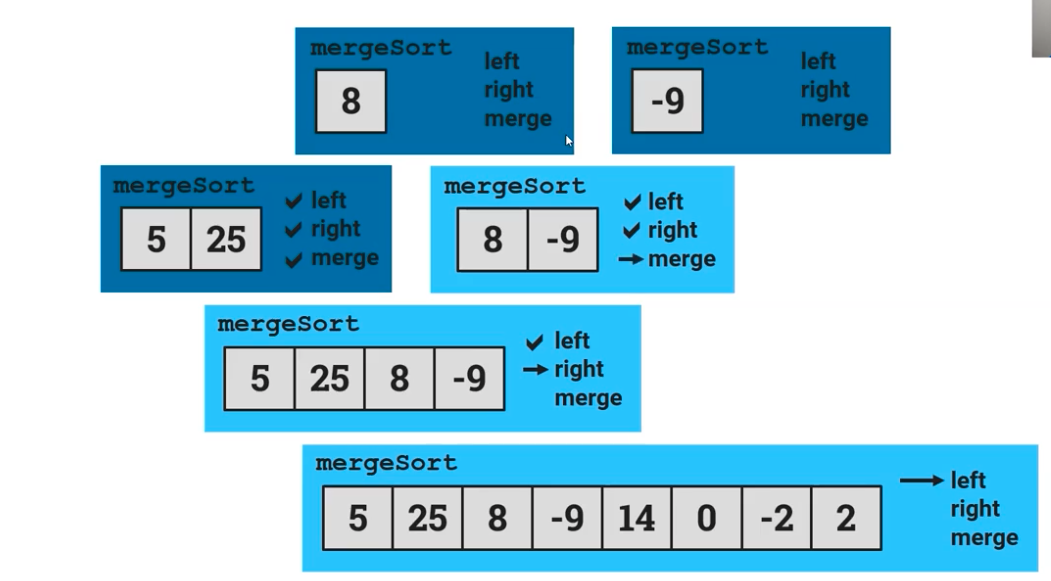
After this, the mergeSort() sorts -9 and 8 into the right order, and then recurses it once again 8 and -9 with the sorted -9 and 8 instead.
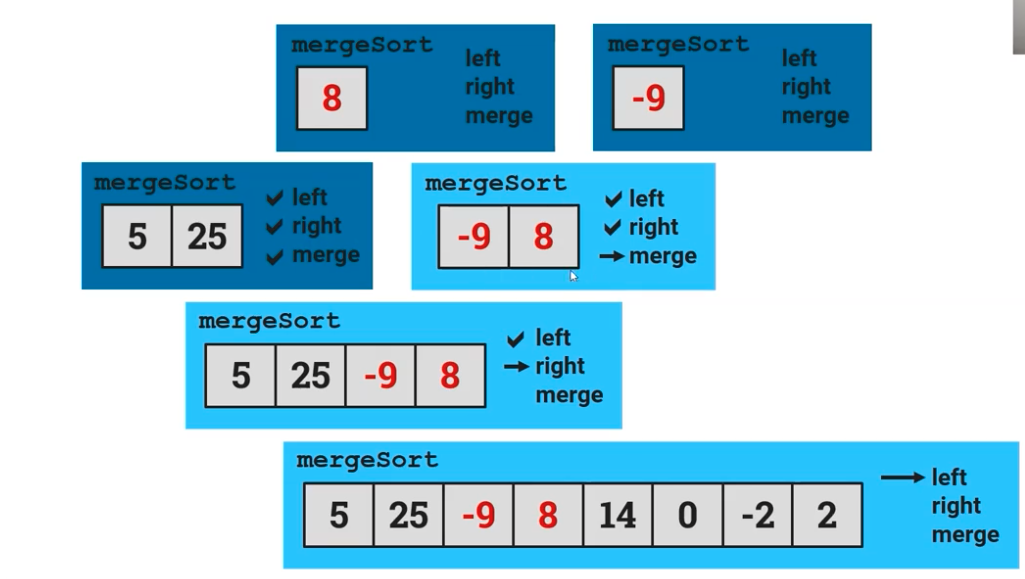
Because the four of the numbers for the left side of the original list were not in the correct order overall, mergeSort is once again called and the list is sorted with the correct order for just the left side, now containing -9, 5, 8, 25.
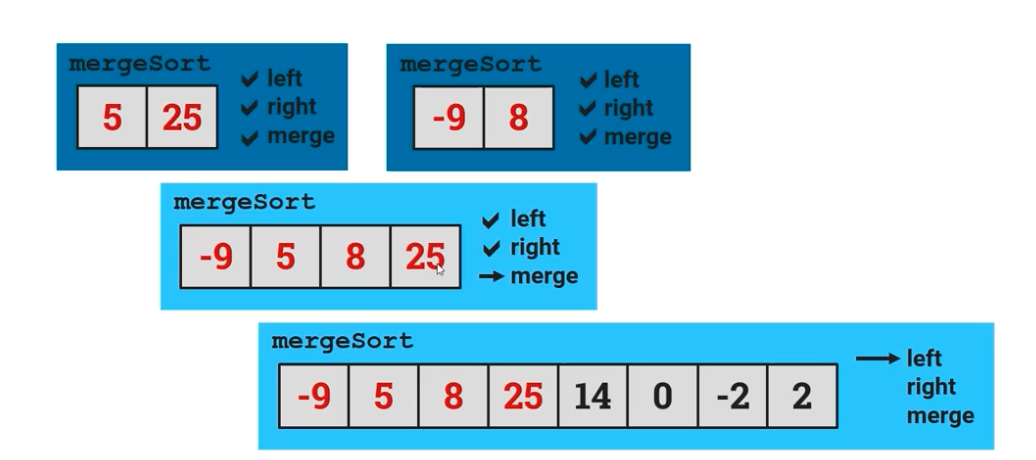
This process is then repeated, but for the right half of the ArrayList. It keeps slitting the list in half, sorting it, and then bringing it to the level below, where eventually, the ArrayList is sorted and merged together, as shown in the image below.
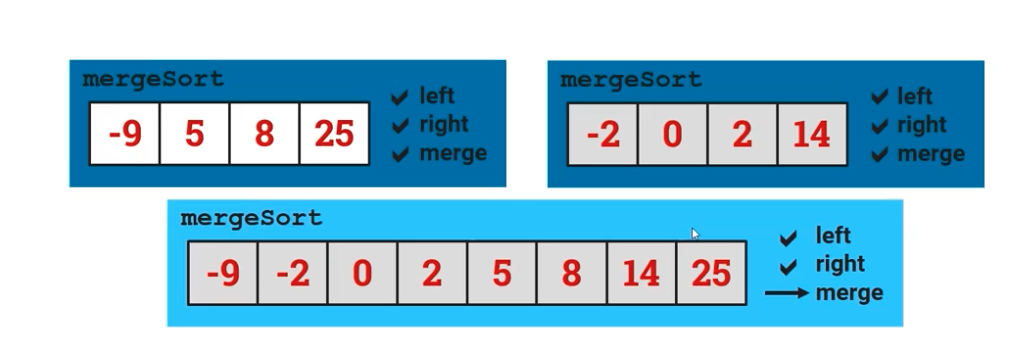
This is a code segment that CollegeBoard had provided in order to see the recursion behind mergeSort(). The code calls mergeSort() on itself in order to sort the list and merge the halves until you reach the right order and final list.

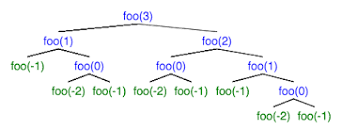
Recursion Trees
Recursion trees are a method for visualizing each recursive case (everytime the method is called) until the base case is reached.
Recursive blocks call themselves. In order for them to finish, there must be some special case in which they don't call themselves. That is the base case, a simpler version of the block's script that doesn't call the block itself.
There is usually a conditional with two cases: a base case for the lowest level that stops the recursion from going on forever and a recursive case that calls the block itself at lower levels until it reaches the base case.
Note: If a block keeps recursively calling itself forever, the program is stuck in an infinite loop meaning that there isn't a base case or it is not accessible.
public class example{
static int foo(int n) {
if (n < 0){
return 1;
}
else{
return foo(n-2) + foo(n-1);
}
}
public static void main(String args[]){
System.out.println(foo(3));
}
}
example.main(null);
Class Activity
If you are on the left side of the class, you will be working with the factorial code. If you are on the right side of the class, you will be working with the fibonacci code. The objective is to work with your crossover team to act out the recursion tree for the code segments below. The first team from each side to show up the correct recursion tree will receive candy!
TASK: You and your crossover team must physically act out the recursion tree, meaning standing up and each taking a sticky note to represent each branch of the tree.
If you are on the Fibonacci side: You will be acting out fib(3)
If you are on the Factorial side: You will be acting out fact(4)
// Fibonacci Series using Recursion
class fibonacci {
static int fib(int n)
{
// Handling base case
// iIf value of n=1 or n=0, it returns 1
if (n <= 1)
return n;
// Generic case
// Otherwise we do n-1 + n-2!
return fib(n - 1) + fib(n - 2);
}
public static void main(String args[])
{
// Calling method 1 to compute fibonacci and
// storing the result into a variable
int n = 3;
// Print and display the fibonacci of number
// customly passed as an argument
System.out.println("3rd Fibonacci Sequence is: " + fib(n));
}
}
fibonacci.main(null);
class factorial {
static int fact(int n)
{
// Handling base case
// iIf value of n=1 or n=0, it returns 1
if (n == 0 || n == 1)
return 1;
// Generic case
// Otherwise we do n*(n-1)!
return n * fact(n - 1);
}
// Method 2
// main driver method
public static void main(String[] args)
{
// Calling method 1 to compute factorial and
// storing the result into a variable
int n = 4;
// Print and display the factorial of number
// customly passed as an argument
System.out.println("Factorial of 4 is: " + fact(n));
}
}
factorial.main(null);